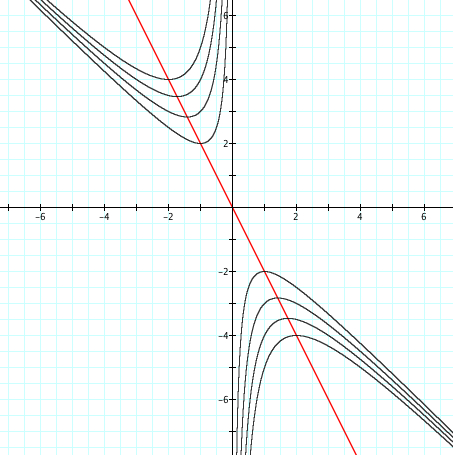
The Manipulation of C
C was after all the correct choice. One can see from the table below that C moves the graph up and down similair to how my Grandma's flower beds were laid.
| 1 | 2 | 3 | 4 |
|---|---|---|---|
 |
 |
 |
 |
What was left to find was the minimums of the curves on the left. From what we can see we know that the graphs are almost like reflections of one another so the minimums of the first curve will be the same as the maximum on the securve just multiply each coordinate by a negative 1. This means that the line of reflection for the curves is y = x. This means that if I find the line that the minimums go through then that line will also be the one that the maximums go through. To be completely honest at this point I was lost on how to find this minimum, so I resorted to the old fashion method of tracing. With this I found the minimum when c=1 to be at the point (-1, 2). I figured at this point I would try different values of c until I found another good whole point like that one as that would make figuring out the function a little easier. I ended up with the table below after hours of gruelling work.
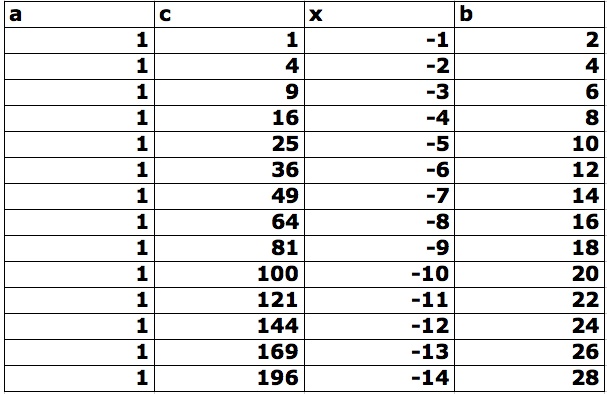
I noticed a couple of interesting patterns after completing this chart. First one was with column c, we have 1 + 3 = 4, then 4 + 5 = 9, then 9 + 7 = 16, then 16 + 9 = 25, so forth and so on. So what is happening is that we are always adding on the next odd number starting with 3. This pattern was incredibly helpful in finding the minimums for the curve because it also gave us a minimum with whole number coordinates, which also followed a pattern. The x column goes in order taking one away each time, however the b column is always increasing by two. This helped me in figuring out the function of the line where all the minimums and maximums would be.
We need an equation where something happens to x in order to get b. With this in mind I was able to find find that the function is simply f(x) = -2x. We plug in any one of the ones in the column x and we will get the corresponding b.
So together we get our locus with the possible graphs for Grandma's design: